Salutare! Am o neclaritate in legatura cu radicalii de ordin n. Daca am radical de ordin 2 din 9, atunci solutia este 3, deoarece din definitia radicalului de ordin n (n=2k,in acest caz). Dar, dece nu luam in considerare si solutia -3? Nu o luam, pentru ca definitia spune ca radicalul unui numar este un numar unic? Sau din alte considerente? Confuzia mea pleaca de la faptul ca atunci cand, de exemplu, rezolvam o ecuatie de gradul II, consideram + sau – radical din delta, adica luam in considerare ambele cazuri. Stiu ca neintelegerea mea poate parea stupida pentru unii, dar chiar am nevoie sa inteleg conceptul. Deci, rezumand, consideram doar o solutie deoarece prin definite radicalul unui numar este un nr unic, sau exista si alte considerente? Multumesc!


Eu as zice ca da, unicitatea radicalului determina acest lucru.
Pe de alta parte, ecuatia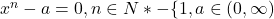
are o singura solutie reala pozitiva, deci exista un numar unic x astfel in cat x ridicat la o putere n sa fie egal cu a. Daca vrei sa descoperi mai mult, te poti documenta despre multimea numerelor reale, care are niste proprietati deosebite ce se studiaza abia in clasa a 12-a, dar din care rezulta aceasta unicitate. Intr-o enciclopedie matematica de prin ’80 am vazut ca exista asa ceva.