Aratati ca:
![]()
Am incercat sa grupez termenii cite 4, cite 5, cite… astfel incit sa pot sa obtin ceva egal cu un produs de 105 (ca, similar, aici: http://forum.matematic.ro/viewtopic.php?t=20387) dar…nimic!
Orice ajutor e binevenit. Multumesc!


Sigur nu exista si un 2 la 0 pt ca suma ta este un nr par care nu se poate divide cu divizorii lui 105=3*5*7 ????
Multumesc de raspuns diamond.
Acum am verificat enuntul postat si l-am copiat corect din manual.
Primul 2 e 2 „chior” (ma rog, la puterea 1 daca vreti).
Si-acuma, ca mi-ai raspuns, … da, ar fi trebuit sa-mi sara-n ochi ca suma rezultata e un numar par care…
Daca are vreo importanta/relevanta exercitiul este luat din „Culegere de probleme de matematica pentru clasa a VI-a” (a.k.a. „Pui”) de Manea Ioana Monalisa si Neagoe Cristina, Bucuresti, Ed. Logos Jr., 2012.
EDIT:
Cu toate ca, n-are nici-o importanta ca suma e un numar par!!!
Daca, prin absurd, suma ar face, sa zicem, 840, ea se divide cu 105, nu?
Deci?
Enervant:
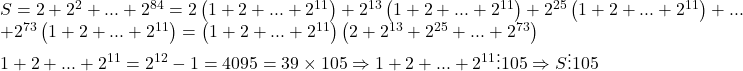
Evident puterea lui 2 am ghicit-o ….
Multumesc diamond si ali pentru solutie!
Daca va spun una: JUR ca m-am oprit cu gruparea termenilor pin’ la
!!!
Am zis ca deja e prea de tot si…
Multumesc.
Nu pot sa nu inchei pina nu remarc, din nou si a n-a oara!!!, ca deja au luat-o rau de tot razna daca la clasa a VI-a au exercitii de genul acesta! Si vorbim de „regular” = manual, nu de Gazeta matematica sau olimpiade sau alte virfuri. In fine…
[list]- Rezolvarea lui diamondminer nu este completa … nu reiese din cele scrie ca neapărat S divide cu 105 ….
- Lucrez la o rezolvare care nu presupune sa calculam 2^12 … adică o rezolvarea cu un rationament mult mai simplu ( nu avem nevoie de calculator de mana) dar mai lunga
🙁
Proaspata (rezolvarea din clasa):
Pentru ca
,
suma trebuie sa se divida simultan cu 3,5 si 7
. (sau cum se va vedea ulterior cu 3×5=15 si 7)
a) se grupeaza cite 3 termeni:
b) se grupeaza cite 4 termeni:
Gata!🙁
Super tare!
Da … la asta m-am referit … însă .. la scoală va învată ceva care nu este tocmai 100% corect:
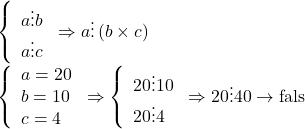
Eu lucrez …. la o demonstratie anume …. o voi publica dacă voi ajunge la vre-un rezultat .
Adevarat ce spui!
Cred ca cel mai corect e:
Se observa ca acea suma are 84 de termeni si cum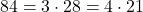 , iar
, iar 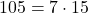 atunci inseamna ca putem grupa termenii cate 3 sau cate 4 obtinand un numar intreg de grupe in fiecare caz.Se observa ca acea suma se mai scrie
atunci inseamna ca putem grupa termenii cate 3 sau cate 4 obtinand un numar intreg de grupe in fiecare caz.Se observa ca acea suma se mai scrie 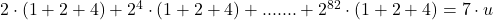 ceea ce inseamna ca acea suma se divide cu
ceea ce inseamna ca acea suma se divide cu  .Grupand similar cate patru termeni se observa imediat ca acea suma se divide si cu
.Grupand similar cate patru termeni se observa imediat ca acea suma se divide si cu  si deci acea suma se divide cu
si deci acea suma se divide cu 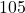 .
.