Home/ Intrebari/Q 78145
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

Visu2412
Pe: 2012-09-30T11:55:24+03:00 In: In:

Inegalitate…

Buna. Am dat de problema asta si nu am reusit sa ii dau de capat.

Fie x,y,z 3 numere reale strict pozitive astfel incat:
x+y+z>=\frac{1}{x}+\frac{1}{y}+\frac{1}{z}.
Sa se arate ca \frac{x+y+1}{x+y+z^2}+\frac{y+z+1}{y+z+x^2}+\frac{x+z+1}{x+z+y^2}<=3.

Am reusit sa demonstrez doar ca x+y+z>= 3
Multumesc anticipat.

Similare

6 raspunsuri

  1. gunty
    maestru (V)

    Abia astept sa vad o rezolvare. Cred ca la problema asta m-am chinuit si eu vreo doua zile, dar tot n-am reusit sa o rezolv. E din gazeta matematica?

  2. Visu2412

    Da.. Am facut in felul urmator.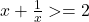
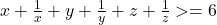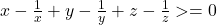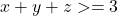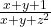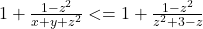    Stiu ca x+\frac{1}{x} >= 2, dupa care am zis ca x+\frac{1}{x}+y+\frac{1}{y}+z+\frac{1}{z} >= 6. Dar din ipoteza, x-\frac{1}{x}+y-\frac{1}{y}+z-\frac{1}{z} >= 0.Am adunat relatiile si mi-a dat x+y+z >= 3. Dupa aceea, am analizat o singura fractie din cerinta, si anume am rescris\frac{x+y+1}{x+y+z^2} ca 1 + \frac{1-z^2}{x+y+z^2} <= 1+\frac{1-z^2}{z^2+3-z} si am aplicat modificarea pentru toate cele 3 fractii. De aici m-am blocat…….

  4. gunty
    maestru (V)

    Am ajuns si eu la ea, insa urmatoarea inegalitate nu e mereu adevarata:

        \[ \begin{array}{l} 1 + \frac{{1 - z^2 }}{{x + y + z^2 }} \le 1 + \frac{{1 - z^2 }}{{z^2 + 3 - z}} \\ \Leftrightarrow \frac{{1 - z^2 }}{{x + y + z^2 }} \le \frac{{1 - z^2 }}{{z^2 + 3 - z}} \\ \end{array} \]

    Fie numerele reale pozitive x=1, y=3, z=2.
    In cazul acesta iti iese ca

        \[ - 0.375 \le - 0.6 \]

    , ceea ce e fals.

  5. Visu2412

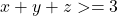    Darx+y+z >= 3, nu? Iar atunci x+y>=3-z.

  6. Visu2412

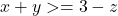    Ar mai fi ceva. Din inegalitatea mediilor \Rightarrow \frac{1}{x}+\frac{1}{y}+\frac{1}{z} \geq 3*[\sqrt[3]{{\frac{1}{x*y*z}}}], dar x+y+z \geq \frac{1}{x}+\frac{1}{y}+\frac{1}{z} \Rightarrow (x+y+z)*[\sqrt[3]{{x*y*z}}] \geq 3 \Leftrightarrow 3*[\sqrt[3]{{x*y*z}}] \geq 3 \Leftrightarrow [\sqrt[3]{{x*y*z}}] \geq 1.

  8. gunty
    maestru (V)

    da, x+y+z>=3 e adevarat, insa inegalitatea discutata de aceea nu e mereu adevarata, pt ca 1-z^2 poate fi si negativ, poate fi si pozitiv, si asta „schimba”
    semnul intre ele. Dar daca iei valoarea absoluta a celor doi, atunci chiar e adevarata, insa asta nu cred ca ne-ar ajuta.

    Din

        \[ \sqrt[3]{{xyz}} \ge 1 \]

    iese ca si

        \[ xyz \ge 1 \]

    , dar tot nu e deajuns.

    Sper ca va veni cineva cu o idee stralucitoare, care va rezolva problema.

Raspunde

Raspunde