Home/ Intrebari/Q 78008
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

Sarah
Pe: 2012-09-20T13:16:17+03:00 In: In:

algebra..

sa se aduca la forma cea mai simpla:
e(x)=[radical din x+(2 radical din x-1)] +[radical din x-(2 radical din x -1)] ???

Similare

14 raspunsuri

  1. PallMall

        \[ E\left( x \right) = (\sqrt x + 2\sqrt {x - 1} ) + (\sqrt x - 2\sqrt {x - 1)} \]

    asta e exercitiul, am scris corect, sa stiu daca rezolv ce trebuie?
    sau

        \[ E\left( x \right) = \sqrt {x + 2\sqrt {x - 1} } + \sqrt {x - 2\sqrt {x - 1} } \]

  2. Sarah

    x apartine [1;2]

  4. Sarah

    nu,este radical dublu,acei 2 radical din x +-1 sunt sub acel prim radical din x

  5. PallMall

    adica

        \[ E\left( x \right) = \sqrt {x + 2\sqrt {x - 1} } + \sqrt {x - 2\sqrt {x - 1} } \]

    asa nu?
    edit : incerc sa rezolv acum.
    Se cere doar sa se aduca la forma cea mai simpla?

  6. Sarah

    a doua varianta este cea buna..
    da,asa,multumesc mult ca ma ajutati
    da,doar la forma cea mai simpla

  8. Sarah

    numai sa se aduca la cea mai simpla forma si il da pe x apartine[1;2]..

  9. PallMall

    Din conditiile de existenta ale radicalilor ajungi la intervalul de definitie care l-ai spus [1,2] parca , nu am verificat
    Eu am facut asa , nu stiu cat de corect este dar ti-o postez:

        \[ \begin{array}{l} a = \sqrt {x + 2\sqrt {x - 1} } \\ b = \sqrt {x - 2\sqrt {x - 1} } \\ ab = x - 2 \\ a^2 + b^2 = 2x \\ (a + b)^2 = a^2 + 2ab + b^2 \\ a + b = \sqrt {a^2 + 2ab + b^2 } \\ a + b = \sqrt {2x + 2(x - 2)} = 2\sqrt {x - 1} \\ \end{array} \]

    Am verificat rezultatul , adica forma cea simpla si merge cu 2,5,10..etc dar nu inteleg de ce nu merge cu 1 , daca vede cineva vre-o greseala sa corecteze , altfel nu stiu cum sa aduci la forma mai simpla.

  10. GreatMath
    veteran (III)

    \begin{array}{l} E\left( x \right) = \sqrt {x + 2\sqrt {x - 1} } + \sqrt {x - 2\sqrt {x - 1} } \\ \sqrt {x + 2\sqrt {x - 1} } = \sqrt {{{\sqrt {x - 1} }^2} + 2\sqrt {x - 1} + 1} = \sqrt {{{\left( {\sqrt {x - 1} + 1} \right)}^2}} = \left| {\sqrt {x - 1} + 1} \right|\\ \sqrt {x - 2\sqrt {x - 1} } = \sqrt {{{\sqrt {x - 1} }^2} - 2\sqrt {x - 1} + 1} = \sqrt {{{\left( {\sqrt {x - 1} - 1} \right)}^2}} = \left| {\sqrt {x - 1} - 1} \right|\\ E = \left| {\sqrt {x - 1} + 1} \right| + \left| {\sqrt {x - 1} - 1} \right| \end{array}
    Exercitiul este relativ… fiind vb de module … se discuta solutia problemei pe intervalul [1,2]

  12. PallMall

    @GreatMath ce zici de rezolvarea mea? Ar avea acelasi rezultat ca al tau daca nu ai avea module , cred ca am sarit vre-un modul pe undeva de nu am ajuns tot acolo

  13. Sarah

    @GreatMath deci ajung si la formula (a+b) la patrat…multumesc pentru ajutor!!

  14. GreatMath
    veteran (III)

    PallMall: solutia ta este incompleta … defapt este în proportie de 99% gresita pe intervalul [1,2] ….. când este vorba de radicalii situatia devine „strange” d.p.d.v matematic …. trebuie neapărat lucrat cu modelul standard … adică noduli…
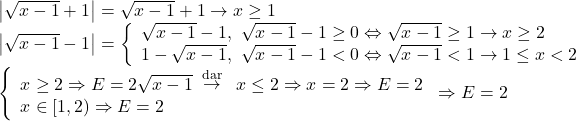
    Completarea la solutia mea ar fi :
    \begin{array}{l} \left| {\sqrt {x - 1} + 1} \right| = \sqrt {x - 1} + 1 \to x \ge 1\\ \left| {\sqrt {x - 1} - 1} \right| = \left\{ \begin{array}{l} \sqrt {x - 1} - 1,\,\,\sqrt {x - 1} - 1 \ge 0 \Leftrightarrow \sqrt {x - 1} \ge 1 \to x \ge 2\\ 1 - \sqrt {x - 1} ,\,\,\sqrt {x - 1} - 1 < 0 \Leftrightarrow \sqrt {x - 1} < 1 \to 1 \le x < 2\, \end{array} \right.\\ \left\{ \begin{array}{l} x \ge 2 \Rightarrow E = 2\sqrt {x - 1} \,\,\mathop \to \limits^{{\rm{dar}}} \,\,\,\,x \le 2 \Rightarrow x = 2 \Rightarrow E = 2\\ x \in \left[ {1,2} \right) \Rightarrow E = 2 \end{array} \right. \Rightarrow E = 2 \end{array}
    Adică pt orice x din [1,2] E va avea valoarea 2 ….. ciudat NU!

  16. GreatMath
    veteran (III)

    Sarah wrote: @GreatMath deci ajung si la formula (a+b) la patrat…multumesc pentru ajutor!!


    Nu stiu ce ai vrut sa zici dar poti copia linistit/a solutia mea+completarea 😀 ….
    Ps: sper ca nu am gresit undeva la calcule 🙂

  17. Sarah

    nu inteleg de ce nu poate avea valoarea 2?? si de ce in ultima acolada este [1;2) si nu [1;2]..?

  18. GreatMath
    veteran (III)

    nu inteleg de ce nu poate avea valoarea 2??


    :confused: E=2 pt orice x din [1,2]

    si de ce in ultima acolada este [1;2) si nu [1;2]..?


    Conditia de explicitare a modulului …..

Raspunde

Raspunde