Buna seara! Am incercat sa rezolv o inegalitate, dar nu am reusit sa ii dau de capat nicicum. Imi puteti da va rog vreo idee?
Fie a,b,c 3 numere reale pozitive cu ![]() .Sa se arate ca
.Sa se arate ca ![]() oricare ar fi n>=2.
oricare ar fi n>=2.
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Fie a,b,c 3 numere reale pozitive cu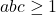 .Sa se arate ca
.Sa se arate ca 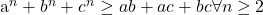 .
.
Pt n= 2 inegalitatea este usor de demonstrat:
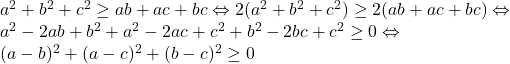
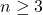 vom demonstra ca
vom demonstra ca 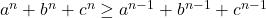
Am obtinut ceva adevarat. Pentru
Vom folosi inegalitatea lui Cebasev pentru tripletele: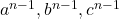 si
si 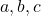
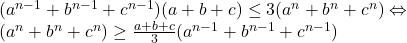
![Rendered by QuickLaTeX.com \frac{a+b+c}{3}\geq \sqrt[3]{abc}\geq1\text{din ipoteza}](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-64d3f9a5d5730779e1ffb7d05286c3ff_l3.png)
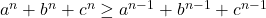
Avem
Si acum folosim inegalitatea mediilor:
obtinem
Pare cam ciudat formalismul pe internet. Eu personal nu tin la el dar raspund cu acelasi tip de respect. Observatia e justa pe care ati facut-o. Si nu stiu acum ce sa fac: sa ma gandesc la o alta solutie sau sa incerc sa rezolv cazul particular ?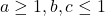
Apreciez interventia si sunt foarte curios sa vad o solutia corecta si completa. Sa speram ca o sa apara…
Domnule… totusi m-am mai gandit… nu e nicio problema cu cazul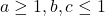
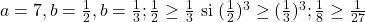
De exemplu :
Deci cele doua triplete au aceeasi monotonie. Gresec undeva?
O idee:
In conditiile date de problema putem scrie