Home/ Intrebari/Q 77088
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

cristyghy96
Pe: 2012-06-04T09:27:17+03:00 In: In:

sisteme de ecuatii

sa se determine valorile lui a real astfel incat sistemul

{x^2+y^2=z, x+y+z=a ; sa aiba solutie reala unica

Similare

5 raspunsuri

  1. Zeus
    veteran (III)

    Asha si dc n-ai rezolvat-o? ce e asha greu? Arata mai intai ce-ai rezolvat tu… ca noi rezolvitorii sa te ajutam mai departe…(face parte din regulament)

  2. PhantomR
    expert (VI)

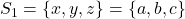    Se poate observa ca schimband x cu y obtinem acelasi sistem, deci sistemul este simetric in variabilele x,y. Atunci daca S_1=\{x,y,z\}=\{a,b,c\} este o solutie, atunci si 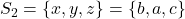S_2=\{x,y,z\}=\{b,a,c\} este o solutie. Rezulta x=y, caci altfel, daca avem o solutie, sistemul va avea inca una diferita de prima, ceea ce contrazice cerinta.

    Avem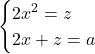 \begin{cases}2x^2=z \\ 2x+z=a\end{cases}. Inlocuind in a doua ecuatie vom avea 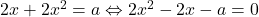2x+2x^2=a \Leftrightarrow 2x^2-2x-a=0. Deoarece x\in\mathbb{R} si solutia trebuie sa fie unica, trebuie sa avem \Delta=0 \Leftrightarrow (-2)^2-4\cdot 2 \cdot (-a)=0 \Leftrightarrow 4+8a=0 \Leftrightarrow a=-\frac{4}{8}=-\frac{1}{2}.

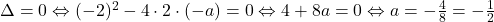    Sa verificam. Avem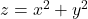 z=x^2+y^2 si inlocuind in 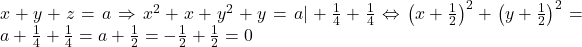x+y+z=a \Rightarrow x^2+x+y^2+y=a |+\frac{1}{4}+\frac{1}{4} \Leftrightarrow \left(x+\frac{1}{2} \right)^2 + \left(y+\frac{1}{2} \right)^2 = a+ \frac{1}{4}+\frac{1}{4}=a+\frac{1}{2}=-\frac{1}{2}+\frac{1}{2}=0, de unde rezulta 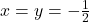x=y=-\frac{1}{2} si apoi, inlocuind in una din ecuatiile initiale ale sistemului, z=\frac{1}{2}.

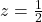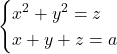    Asadar, singura valoare a parametrului real a pentru care sistemul \begin{cases} x^2+y^2=z \\ x+y+z=a \end{cases} are solutie unica este a=-\frac{1}{2}, pentru care se obtine solutia S=\{x,y,z\}=\left\{-\frac{1}{2},-\frac{1}{2},\frac{1}{2}\right\}.

  4. Zeus
    veteran (III)

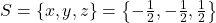    Nu ai rezolvat-o bine… Nu se foloseste simetria aici… pierzi solutii.

  5. PhantomR
    expert (VI)

    Unde le pierd? Zice solutie unica 🙂.

  6. Zeus
    veteran (III)

    Pardon am calculat eu gresit… dar nu tb sa-i faci prb… tb sa astepti sa-si spuna el calculele.

Raspunde

Raspunde