Home/ Intrebari/Q 76379
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

asdf
Pe: 2012-03-25T10:52:26+03:00 In: In:

functie

sa se arate ca oricare ar fi a, b, c reale graficul functiei intersecteaza axa Ox. f:R\{a, b, c}→R, f(x)= 1/(x-a) + 1/(x-b) + 1/(x-c).

Punem conditia ca ∆≥0, dar nu stiu sa aduc functia la forma ei normala. Am dat factor comun dar la numitor imi da functie de gradul 3

Similare

5 raspunsuri

  1. PhantomR
    expert (VI)

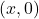    Nu cred ca merge mereu cu \Delta. Orice punct de pe axa Ox are coordonatele (x,0). Atunci, conditia ca un punct 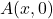A(x,0) sa fie pe graficul functiei este f(x)=0. Trebuie deci sa aratati ca ecuatia f(x)=0 are cel putin o solutie din domeniul de definitie.

    Mai exact ce factor comun ati dat? Banuiesc ca va refereati la numitorul comun.

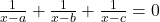    EDIT: Ecuatia f(x)=0 este echivalenta cu \frac{1}{x-a}+\frac{1}{x-b}+\frac{1}{x-c}=0 sau, prin aducere la numitorul comun 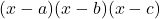(x-a)(x-b)(x-c), avem 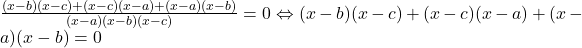\frac{(x-b)(x-c)+(x-c)(x-a)+(x-a)(x-b)}{(x-a)(x-b)(x-c)}=0 \Leftrightarrow (x-b)(x-c)+(x-c)(x-a)+(x-a)(x-b)=0. Desfaceti parantezele, grupati si ar trebui sa va iasa o ecuatie de gradul doi. Puteti folosi Delta apoi 🙂.

    EDIT2: Desfacem parantezele si grupam si ar trebui sa iasa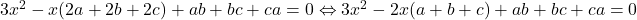 3x^2-x(2a+2b+2c)+ab+bc+ca=0 \Leftrightarrow 3x^2-2x(a+b+c)+ab+bc+ca=0. Avem 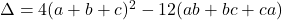\Delta = 4(a+b+c)^2-12(ab+bc+ca). Trebuie sa aratam 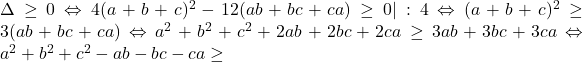\Delta \geq 0 \Leftrightarrow 4(a+b+c)^2-12(ab+bc+ca)\geq 0 |:4 \Leftrightarrow (a+b+c)^2\geq 3(ab+bc+ca) \Leftrightarrow a^2+b^2+c^2+2ab+2bc+2ca\geq 3ab+3bc+3ca \Leftrightarrow a^2+b^2+c^2-ab-bc-ca\geq. Inmultim acum cu 2 si grupam astfel 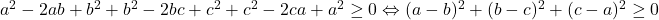a^2-2ab+b^2+b^2-2bc+c^2+c^2-2ca+a^2 \geq 0 \Leftrightarrow (a-b)^2+(b-c)^2+(c-a)^2\geq 0, adevarat, caci patratul unui numar real este \geq 0. 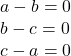Egalitatea are loc daca si numai daca toate patratele anterioare devin nule, adica a-b=0 \\ b-c=0 \\ c-a = 0[tex]\Leftrightarrow a=b=c[/tex].

  2. asdf

    Uitasem de punctul A(x, 0). 😕 Mi-a dat 3x^2-2(a+b+c)-(ac+ab+bc). Multumesc pentru raspuns si o zi buna 🙂

  4. PhantomR
    expert (VI)

    Cu foarte multa placere! Cred ca v-a dat bine (desi cred ca la redactare ati omis un x 🙂).

    Va multumesc si va doresc si eu o zi minunata!:) Sper ca v-ati descurcat si mai departe.

    P.S Am scris si continuarea mai sus.

  5. Bogdan Stanoiu
    maestru (V)

    asdf wrote: sa se arate ca oricare ar fi a, b, c reale graficul functiei intersecteaza axa Ox. f:R\{a, b, c}→R, f(x)= 1/(x-a) + 1/(x-b) + 1/(x-c).

    Punem conditia ca ∆≥0, dar nu stiu sa aduc functia la forma ei normala. Am dat factor comun dar la numitor imi da functie de gradul 3


    Probabil ca trebuie pusa conditia suplimentara ca a;b;c sa fie distincte doua cate doua sau macar distincte.

  6. Bogdan Stanoiu
    maestru (V)

    asdf wrote: sa se arate ca oricare ar fi a, b, c reale graficul functiei intersecteaza axa Ox. f:R\{a, b, c}→R, f(x)= 1/(x-a) + 1/(x-b) + 1/(x-c).

    Punem conditia ca ∆≥0, dar nu stiu sa aduc functia la forma ei normala. Am dat factor comun dar la numitor imi da functie de gradul 3


    Cand vei ajunge in clasa a XI-a incearca sa generalizezi aceasta problema-
    -daca n>1 este unn numar natural si a(1);a(2);..;,a(n) sut numere reale distincte doua cate doua atunci graficul functiei
    f:R-{a(i);i=1,..,n}->R,
    f(x)=1/(x-a(1))+1/(x-a(2))+…+1/(x-a(n)) intersecteaza axa OX (multimea de intersectie are cel putin n-1 puncte)

    Exista vreo demonstratie la nivelul clsei a IX-a pentru generalizare ?

Raspunde

Raspunde