Fie punctele A si B avand afixele zA=1+i si zB=-1+3i. Determinti planul complex punctele C astfel incat triunchiurile ABC sa fie echilaterale. Cum se rezolva?
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Fie punctele A si B avand afixele zA=1+i si zB=-1+3i. Determinti planul complex punctele C astfel incat triunchiurile ABC sa fie echilaterale. Cum se rezolva?
Pai daca ABC este echilateral atunci AB=BC=AC, deci :
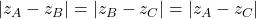
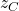
Iei primele doua si ultimele doua de exemplu si il calculezi pe
Latura AB a triunghiului va fi; Zb-Za=-1+3.i-1-i=2.(-1+i)=2.(radical din 2).[(-1/(radical din 2))+i.(1/(radical din 2))]=2.(radical din 2)(cos(3.pi/4)+i.sin(3.pi/4)). Cum intre laturile unui triunghi echilateral, unghiul este de ;(pi/3), determinarea varfului C, se pate face prin rotirea laturii AB cu (pi/3) in sens trigonometric, (o varianta), sau in sens invers trigonometric(o alta variabila). Rotirea se poate face prin inmultirea laturii AB cu ;
(cos(pi/3)+i.sin(pi/3)), deci ; AC=2.(radical din 2).(cos(3pi/4)+i.sin(3.pi/4))
.(cos(pi/3)+sin(pi/3))=2.(radical din 2).(cos(13.pi/12)+i.sin(13.pi/12))=2.(radical din 2).(-1).(cos(pi/12)+sin(pi/12))= Zc-Za , sau ;Zc=1+i-2.(radical din 2).(1/2).{[(radical din 3)+2]/2+[(radical din 3)-2]/2}=
[-(radical din 3)-2+(radical din 2)]/(radical din 2)+i.[-(radical din 3)+2+(radical din 2)]/(radical din 2)–>pentru prima variabila.
In cazul a celei de a doua varianta, vom avea; AC’=Zc’-Za=2.(radical din 2).(cos(3.pi/4)+i.sin(3.pi/4)). (cos(-pi/3)+isin(-pi/3))=2.(radical din 2).
(cos(5.pi/12)+i.sin(5.pi/12)=2.(radical din 2).(1/2).{[(radical din 3)-2]/2+
[(radical din 3)+2]/2}, De unde ; Zc’={[(radical din 3)-2+(radical din 2)]/(radical din 2)+i.[(radical din 3)+2+(radical din 2)]/(radical din 2)}
Multumesc!