E11.
Se da
![]()
![]()
Sa se det. a,b ![]() R astfel incat
R astfel incat
![]() si
si
![]()
E12
Fie functia ![]()
Sa se determine m apartine R
a)multimea ![]() sa fie formata dintr-un singur punct.
sa fie formata dintr-un singur punct.
b)
![]() in doua puncte distincte
in doua puncte distincte
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Va rog frumos ca inainte sa postati sa apasati butonul „Preview” pentru a vedea cum va arata postul.
E11: Trebuie sa determinati astfel incat
astfel incat  .
. din cauza conditiei de existenta a fractiei anterioare) si
din cauza conditiei de existenta a fractiei anterioare) si 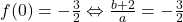 .
. sau, folosind-o pe a doua,
sau, folosind-o pe a doua,  , de unde
, de unde  . Inlocuind, de exemplu, in cea de-a doua ecuatiei se obtine
. Inlocuind, de exemplu, in cea de-a doua ecuatiei se obtine  .
.
(NOTA: A se avea in vedere faptul ca
Prima ecuatie se mai scrie:
E12: are o singura solutie
are o singura solutie  are
are ![Rendered by QuickLaTeX.com \Delta=0 \Leftrightarrow [-(2m-1)]^2-4(m+1)(m+1)=(2m-1)^2-4(m+1)^2=4m^2-4m+1-4m^2-4m-4=-8m-3=0 \Leftrightarrow m=-\frac{3}{8}](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-9328759c2c6d3ba52dca22eefc760948_l3.png) .
.
a) Conditia din enunt este echivalenta cu faptul ca ecuatia
b) Condtia este echivalenta cu faptul ca ecuatia de mai sus are
1]. Pentru ; Gf intersectat cu OX , in A(a, 0), vom avea; f(a)=0 , sau ;
(2.a^2+b+2)/(2.a)=0 , sau ; 1]. a+(1/2).(b+2)/a=0.
Pentru ; Gf. intersectat cu OY , in B(0 , -3/2) , vom avea; 2]. f(0)=(b+2)/a=-3/2 , Din 1]. si 2]. determinam pe a si pe b.
2]. a]. Ca Gf. sa taie pe OX intr-un punct , trebue ca „discriminantul”lui
f(x,m) sa fie zero . ; (2.m-1)^2-4.(m+1)^2=0, de unde se deduce „m”.
b]. Ca Gf.sa taie pe OX in doua puncte distincte , trebue ca discriminantul lui f(x,m) sa fie mai mare ca zero. si „m” se determina din aceasta inegalitate.