Sa se studieze bijectivitatea functiei:
f:[0,+∞)→(-∞.4] , f(x)=max(3-x, 1-x/3)
O astfel de problema se rezolva numai grafic?
Multumesc
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Asa arata relatia de definitie: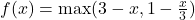 ? (ar putea exista o confuzie in privinta fractiei de aceea intreb)
? (ar putea exista o confuzie in privinta fractiei de aceea intreb)
Da este corecta fractia.
Ok. Multumesc!Atunci avem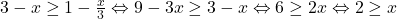 . Analog,
. Analog, 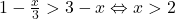 . Asadar functia este:
. Asadar functia este: 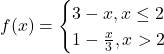 .
.
Consideram functiile![Rendered by QuickLaTeX.com g:[0,2]\rightarrow\mathbb{R}](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-8fee542dbde7e76b6d75ad3a33ea849b_l3.png) si
si 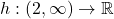 definite astfel
definite astfel 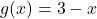 ,
, 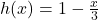 .
.
Functia este injectiva daca si numai daca
este injectiva daca si numai daca  injective si
injective si 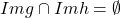 .
.  este surjectiva daca si numai daca
este surjectiva daca si numai daca ![Rendered by QuickLaTeX.com Im g \cup Im h = (-\infty;4]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-159665fa37fff04a89f3ae35adea62a1_l3.png) .
.
Functia
Se verifica daca ambele conditii sunt indeplinite. Va descurcati?:) Daca nu sau daca nu intelegeti sau am gresit ceva va rog sa imi spuneti.
Multumesc ,am inteles,primele conditii nu stiam cum sa le pun.
Cu multa placere! Ma bucur!:)
In legatura cu prima conditie, acea parte cu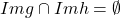 provine din faptul ca daca cele doua imagini ar avea o interesctie nevida, atunci, cum domeniile functiilor
provine din faptul ca daca cele doua imagini ar avea o interesctie nevida, atunci, cum domeniile functiilor  sunt disjuncte, am avea doua valori distincte ale lui
sunt disjuncte, am avea doua valori distincte ale lui  pentru care
pentru care 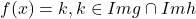 , ceea ce ar conduce la neinjectivitatea functiei
, ceea ce ar conduce la neinjectivitatea functiei  .
.