Sa se arate ca :
![]()
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Cum ambii membri sunt pozitivi, inegalitatea este echivalenta, prin ridicare la patrat, cu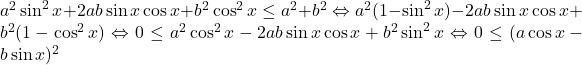 , adevarat.
, adevarat.
OPTIONAL(sau nu?:)):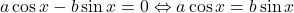 . Daca
. Daca  atunci avem ori
atunci avem ori 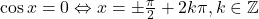 ori
ori  . Daca
. Daca 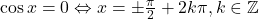 atunci
atunci  sau
sau 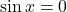 , aceasta din urma fiind imposibila pentru ca nu exista
, aceasta din urma fiind imposibila pentru ca nu exista  real pentru care sa avem
real pentru care sa avem 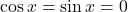 (De ce? Un argument ar fi faptul ca acea egalitate ar implica
(De ce? Un argument ar fi faptul ca acea egalitate ar implica 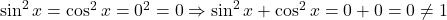 , contradictie cu formula fundamentala a trigonometriei). Daca
, contradictie cu formula fundamentala a trigonometriei). Daca  si
si 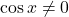 atunci egalitatea are loc pentru
atunci egalitatea are loc pentru 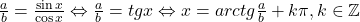 . Asadar avem egalitate pentru
. Asadar avem egalitate pentru 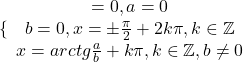 .
.
In plus egalitatea are loc pentru
sau:
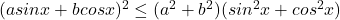 , si cum
, si cum 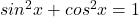 , rezulta concluzia…
, rezulta concluzia…
Din CBS avem:
Intr-adevar, cred ca este mult mai elegant asa. Felicitari!
As aduce totusi o nota. La trecerea sub radical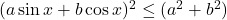 devine
devine 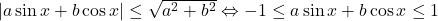 .
.