Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
1.Calculati suma tuturor nr.nat de trei cifre,care impartitela 31 dau restul 13.
2.Aratati ca n este nr. natural,astfel incat nr. n la puterea 2+n+41 sa fie patrat perfect.
3.Demonstrati ca orice n nr. nat. b=2 la puterea n+3 la puterea n+1 +5la puterea n+2 +7 la puterea n+3 nu este patrat perfect.
Te rog sa nu mai postezi probleme diferite in acelasi topic. Nu-ti voi raspunde decat la una dintre probleme si numai dupa ce vom termina cu aceea putem trece si la alta.
Asadar, la problema 1, deoarece nu ai dat nici o informatie despre ce ai facut (gandit) tu inteleg ca nu ai avut nici o idee. Ca urmare iti dau ideea de inceput:
Numerele sunt de forma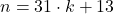
, unde 
poate lua acele valori pentru care 
este numar de trei cifre, adica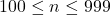 
.
Astept sa imi spui daca reusesti sa continui rezolvarea problemei. Succes!
3.
Se verifica prin calcul ca pentru n<2 nu se obtin patrate perfecte.
Daca n>1 este impar atunci 2^n este divizibil cu 4 , 3^(n+1) ; 5^(n+2) si
7^(n+3) dau restul 1 la impartirea cu 4 si deci in acest caz numarul din enunt da restul 3 la impartirea cu 4.
Daca n>1 este par atunci 2^n este divizibil cu 4 , 3^(n+1) si
7^(n+3) dau restul 3 la impartirea cu 4 iar 5^(n+2) sa restul 1 la impartirea cu 4 si deci si in acest caz numarul din enunt da restul 3 la impartirea cu 4.
Dar orice patrat perfect impar da restul 1 la impartirea cu 4. Deci numarul din enunt nu poate fi patrat perfect.
Observam ca 2;3;5;7 sunt primele 4 numere din sirul numerelor prime. Ar fi interesat de studiat urmatoarea problema. Fie m>1 natural . Exista n>0 natural astfel incat
(p(1))^n+(p(2))^(n+1)…+(p(m))^(n+m-1) sa fie patrat perfect ? . (prin p(k) am notat al k-lea termen al sirului numerelor prime ordonat crescator).
Daca da, care sunt valorile lui m pentru care exista un astfel de n ?
Cine are idei ?
si numarul 2? eu nu am gasit