1. Sa se arate ca modulul unui numar complex
![]()
,este egal cu 1. Reciproc, sa se arate ca orice numar complex de modul 1 si diferit de -1 poate fi scris in mod unic sub forma:
![]()
.
2.Sa se calculeze modulul si argumentul numarului complex:
![Rendered by QuickLaTeX.com \[ \begin{array}{l} a).\quad z_1 = \frac{1}{{1 + i \cdot tg\;\alpha }}\quad ,\alpha \in R - \left\{ {\frac{{(2k + 1)\pi }}{2}|k \in Z} \right\} \\ \\ b).\quad z_2 = a\frac{{1 + ib}}{{1 - ib}}\;,a,b \in R. \\ \end{array} \]](https://anidescoala.ro/wp-content/ql-cache/quicklatex.com-96359816aa31829f01489f29a8f6ffbe_l3.png)
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
1.

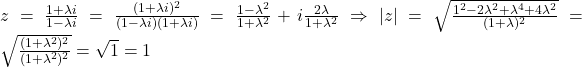 .
.
EXISTENTA: Fie
UNICITATEA: Presupunem prin absurd ca ar exista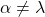 cu
cu 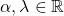 astfel incat astfel incat
astfel incat astfel incat 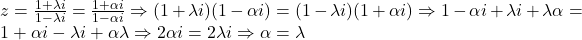 , contradictie. Asadar scrierea este unica.
, contradictie. Asadar scrierea este unica.
2.
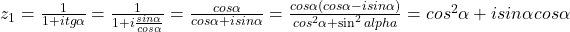 . Cum
. Cum 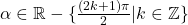 avem
avem 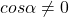 , deci
, deci 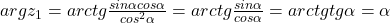 .
.
a)
b)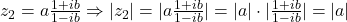 . Am folosit rezultatul de la punctul 1. Demonstratia se gaseste mai sus.
. Am folosit rezultatul de la punctul 1. Demonstratia se gaseste mai sus.
Facand calculele ca la punctul 1. obtinem: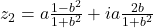 . Daca
. Daca  , atunci
, atunci 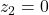 si nu are argument, caci nu exista
si nu are argument, caci nu exista  astfel incat
astfel incat 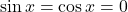 . Daca
. Daca 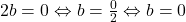 atunci
atunci 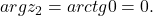 Daca
Daca  si
si 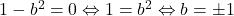 atunci
atunci  este pur imaginar si argumentul sau este:
este pur imaginar si argumentul sau este: 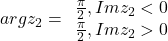 .
.
Excluzand cazurile de mai sus avem: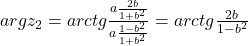 .
.