Home/ Intrebari/Q 70856
Urmator
In Process

AniDeȘcoală.ro Latest Intrebari

sindex
Pe: 2010-11-16T15:38:36+02:00 In: In:

Functie , Taylor.

Ajutati-ma si pe mine va rog cu urmatoarea problema
Mi se da functia :

    $$f(x) = \ln (2 - 3x + {x^2})$$

Cerinta : Folosind dezvoltarea Taylor pentru

    $$\ln (1 + x) = \sum\limits_{n = 0}^\infty {{{( - 1)}^n}} {{{x^{n + 1}}} \over {n + 1}},\forall x \in ( - 1,1]$$

sa rescriu functia f(x) sub forma de serie.
Am prelucrat ln-ul : f(x) = \ln (2 - 3x + {x^2}) = \ln (2 - x) + \ln (1 - x) = \ln (1 + 1 - x) + \ln (1 - x) si folosind formula taylor am rescris functia :

    $$f(x) = \sum\limits_{n = 0}^\infty {{{( - 1)}^n}} {{{{(1 - x)}^{n + 1}}} \over {n + 1}} + \sum\limits_{n = 0}^\infty {{{( - 1)}^n}} {{{{( - x)}^{n + 1}}} \over {n + 1}}$$

    $$ = \sum\limits_{n = 0}^\infty {{{{{( - 1)}^n}} \over {n + 1}}[{{(1 - x)}^{n + 1}}} + {( - x)^{n + 1}}]$$

    $$ = \sum\limits_{n = 0}^\infty {{{{{( - 1)}^n}} \over {n + 1}}} \cdot {( - 1)^{n + 1}}[{(x - 1)^{n + 1}} + {x^{n + 1}}]$$

    $$ = - \sum\limits_{n = 0}^\infty {{{{{(x - 1)}^{n + 1}} + {x^{n + 1}}} \over {n + 1}}} $$

Mai departe nu stiu ce sa fac, va rog, ajutati-ma..vine partialul si trebuie sa stiu cum sa termin acest ex. Multumesc.

Similare

5 raspunsuri

  1. sindex

    va rog, o indicatie ceva…

  2. Sigma2
    maestru (V)

    sindex, din cate -mi amintesc eu, seria taylor se dezvolta intr-un punct xo
    pe care tu nu-l precizezi.cumva xo =0?Atunci ai o serie Mc laurin. Ma uit
    diseara peste ea.

  4. sindex

    pai nu am ce sa precizez in legatura cu el. pur si simplu asa este exercitiul.

  5. Sigma2
    maestru (V)

    Notez f1(x)=ln(2-x) f2(x)=(1-x) f1(x)+f2(x)=ln(1-x)*(2-x)

    dezvoltam functia f1(x) in serie McLaurin (Serii Taylor cu xo=0)

    formula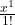
    f(x)=f(xo+\frac{x^1}{1!}*f`(o)+\frac{x^2}{2!}*f„(0)+…+\frac{x^n}{n!}*f^(n)(o) +…. f^(n ) derivata de ordin
    n

    f(0)=ln2

    f1`(x)=-\frac{-1}{2-x} f`(0)=-\frac{1}{2}

    f1„(x)=-\frac{1}{(2-x)^2} f„(0)=-\frac{1!}{2^2}

    …………………………………….
    f(^N)(X)=-\frac{(n-1)!}{(2-x)^n} f^(n)(0)=-\frac{n-1!}{2^n}

    iNtroducem aceste valori in formula si obtinem

    f1(x)=LN(2)-\frac{x*0!}{1!*2^1}–\frac{x^2*1!}{2!*2^2}-…-\frac{(n-1)!*x^n}{2^n*n!}+… <=>
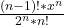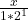    f1(x)=ln2-\frac{x}{1*2^1}–\frac{x^2}{2*2^2}-…-\frac{x^N}{n*2^n}… rel (I)

  6. Sigma2
    maestru (V)

    Pe f2(x)=ln(1-x) il dezvolt dupa formula ta

    f2(x)=\sum_{0}^{oo}[tex]\(-1)^n*\frac{(-x)^{n+1}}{(n+1)}[/tex]=

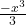    – \frac{x}{1}– \frac{x^2}{2}– \frac{-x^3}{3} -…-\frac{(x)^{n+1}}{n+1}-…. (II)

    f1+f2=ln2-(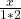\frac{x}{1*2}+\frac{x}{1})-(\frac{x^2}{2*2^2}+\frac{x^2}{2})-….(\frac{x^n}{n*2^n}+\frac{x^n}{n})-\frac{x^{n+1}}{n+1}…=
    ln2-\frac{3x}{1*2}–\frac{5x^2}{2*2^2}–\frac{9*x^3}{3*2^3}-…-\frac{2^n+1*x^n}{n*2^n}…
    sper sa nu fi gresit pe undeva mai verifica situ

Raspunde

Raspunde