Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
In interiorul unui cub cu muchia de 9 se considera 1981 puncte.
Sa se demonstreze ca printre cele 1981 de puncte considerate exista cel putin doua cu proprietatea ca distanta dintre ele este mai mica decat 1.
Impartim cubul in
cubulete de lungime 1.1981>729*2+1 deci intr-un cub(din principiul cutiei)vor exista 3 puncte.Daca acel cub il sectionam dupa diagonala principala in 2,vom avea 2 semicuburi(tetraedre tridreptunghice);
Atunci vom avea ori 2 puncte pe diagonala cubului si un al treilea pe o fata,sau 2 puncte diagonal opuse,si unul interior unuia din semicuburi,sau vom avea 2 puncte in interiorul aceluiasi semicub si oricum am lua situatia,exista 2 puncte intre a caror distanta e cel mult 1.
Presupun ca va referiti la sectiunea dupa un plan diagonal.
Dar oricum, eu spun ca pot exista 3 puncte in interiorul unui cub cu latura de lungime 1 astfel incat toate distantele dintre ele sa fie mai mari de 1. De exemplu, cele trei puncte pot fi foarte apropiate de varfurile cubului ce formeaza un triunghi echilateral cu latura
.
Iata o demonstratie:
Presupunand prin reducere la absurd ca nu ar exista puncte la o distanta mai mica de 1 atunci toate sferele de raza 1/2 cu centrele in cele 1981 de puncte ar avea interioarele disjuncte. Cum toate aceste sfere sunt incluse intr-un cub cu muchia de 10 (am prelungit fiecare muchie cu 1/2 in ambele directii pentru a cuprinde chiar si sferele cu varfurile in puncte aflate pe suprafata cubului), ar rezulta ca suma volumelor sfereloor este mai mica decat volumul cubului cu latura de 10, adica:
,
ceea ce este fals!
Eu cred ca niciunul nu aveti dreptate🙂 ). Putem pune in cubul de muchie 9 cate 10 puncte pe linie, 10 pe coloana si 10 pe „inaltime” =>1000 de puncte. (distantele intre punctele de pe aceeasi linie , coloana si diagonala vor avea lungimea 1 alea adiacente).
Intr-un cub de muchie 1 nu putem sa punem nici un pct in + care sa respecte conditia ca de la el la orice alt varf din cub distanta sa fie mai mare ca 1. Cel mai bun loc unde s-ar putea pune e centrul cubului. Dar nici acolo nu respecta conditia. Diagonala cubului e sqrt(3) iar distanta pana la orice alt punct din cubuletz e sqrt(2)/sqrt(3)<1. Deci eu zic ca acel 1981 e fortat …putea fi chiar 1001.
Banuiesc ca va referiti la primul meu mesaj, in care nu faceam decat sa-i arat lui TheodorMunteanu ca o veriga din rationamentul sau este incorecta. Nu vad in ce fel nu am avut dreptate!
Consider de asemenea ca demonstratia pe care am dat-o in cea de a doua postare nu are niciun cusur. Si din demonstratia mea se vede ca 1981 este fara rost de mare (probabil problema a fost propusa in anul 1981). Se putea lua chiar si 1275, pentru ca
.
O sa ma uit pe demonstratia dvs… dar la primul post ziceati ca 3 pct pot fi puse pe triunghiurile echilaterale de latura sqrt(2). E f dubios ce ati zis. Cu cat se apropie de un punct cu atat distanta scade…si evident scade sub 1, daca ati face figura v-ati da seama sau poate v-ati dat seama deja.
S-ar putea sa trageti concluzii eronate. Am afirmat ca „pot exista 3 puncte in interiorul unui cub cu latura de lungime 1 astfel incat toate distantele dintre ele sa fie mai mari de 1„. Aceasta propozitie este evident adevarata!
Cred ca nu ati inteles de ce am spus aceasta propozitie. Cititi cu atentie postul lui TheodorMunteanu si veti vedea ca in rationamentul sau spunea ca daca 3 puncte apartin interiorului unui cub de muchie 1 atunci obligatoriu doua dintre ele se afla la distanta mai mica de 1. Nu am facut nimic altceva decat sa ii spun ca aceasta deductie este gresita!
Sfera are volumul 4*PI*R^3/3 si tot va da prea mult ptr puncte. Demonstratia poate fi ok dupa ce calculati cu volumul de mai sus dar nu obtineti nr minim de puncte care nu indeplinesc conditia de a fi mai mica distanta decat 1.
Da m-am hazardat am crezut altceva. Aici avetzi dreptate. Suma volumelor sferelor e imposibil sa fie exact 10^3 e mai mica…nu se pot aseza un nr asha de mare de sfere astfel incat sa nu existe spatiu intre ele. Iar acest lucru face sa apara eroarea de precizie in calcul (lucru care inseamna ca pot fi alese un nr mai mic decat 1981 care sa respecte cerinta). Iar ca sa demonstrati ca 1275 e limita tb sa asezati sferele foarte „smecher” si nu cred ca e posibil nici macar atunci.
Greseala mea din al doilea post este impardonabila!
Evident ca stiam volumul sferei dar am dat dovada de o neatentie crasa!
In ce priveste primul post imi mentin parerea ca nu am gresit cu nimic!
Hai ca va iert,🙂 ) dupa ce facetzi cinste cu o shaworma 🙂 ) glumesc 🙂 ) off-topic.
Va rog, nu mai rasuciti cutitul in rana! Acel 1275 se baza pe calculele gresite generate de formula „defectuoasa” a volumului sferei! Parerea mea de rau este cu atat mai mare tinand seama ca refacand calculele, demonstratia ramane valabila:
, ultima fractie fiind aproximativ 3,03 < pi.
Mai bine zis,nu rasuciti cutitul in shaorma.Uite ca dupa 2 ani de la aparitia problemei,am aprins scanteia unde trebuie.
.Dupa asta ar urma sa folosim un alt principiu.Daca 
multimi masurabile si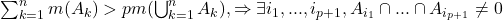
O alta solutie posibila ar fi sa presupunem ca toate punctele se afla la minim distanta 1.Apoi sa formam drepte pe care sa le proiectam pe Ox si pe Oy unde dupa cum o dreapta face cu orizontala un unghi de cel mult 45 respectiv cu verticala tot 45.
Atunci suma proiectiei unui segment
Nu inteleg dc te iei de shaworma mea.
1. Te complici…nu stiu ce vrei sa demonstrezi dar daca vrei sa impresionezi cu cunostintele tale „peste masura” n-o sa-ti iasa fiindca intr-un cub cu muchia de 1 incap maxim 8 puncte aflate chiar in varfurile cubului.
2. Poate vrei sa zici ca-s mai mult de 8 pct…ceea ce e fals. Iar daca e asha (cum si este de fapt) obtzii 1000 pct care satisfac conditia iar 1001 care nu satisfac conditia de a fi la distanta mai mica de 1.
3. E posibil sa iasa si cum zici u dar daca prb se poate rezolva mai simplu nu inteleg dc iti faci singur rau. Chiar daca demonstratia ta e buna tot nu obtzii acel 1000 si acel 1001. (in cel mai fericit caz demonstrezi ca 1981 e exagerat de mare dar mai mult nu).
4. E acelasi lucru totusi…daca iei baza si un cerc de raza 1 obtzii spatiu liber sqrt(2)-1 si daca il inconjori in felul asta obtzii o sfera cu aceasta raza care tot e insuficienta deoarece diametrul e 2*(sqrt(2)-1)<1 deci n-ai facut nimic.
Esti un ganditor bun,blaugranas.
.Demonstreaza ca exista o dreapta ce trece prin interiorul patratului si taie minim 4 segmente,din cele formate de cele 7 puncte.
Dar ce-ar fi sa ma scutesti de observatiile 1,3,4.Mai bine o idee proasta decat nimic,iar tu n-ai facut decat sa critici.Ok,e bine si cu critica,dar adu si o idee constructiva in sensul asta daca tot ti-ai asumat rolul.
Si ca sa nu para ca imi etalez cunostintele degeaba,ideea mea se poate folosi si’n urmatoarele probleme;
Intr-un patrat de latura 1 sunt inscrise un numar finit de segmente de lungime totala 10.Demonstreaza ca exista o dreapta (ce trece prin patrat)ce intersecteaza cel putin 6 astfel de segmente.
Intr-un patrat de latura 1 exista 7 puncte,oricare 3 necoliniare de distanta minima
PS:partea cu shaorma evident era o gluma😉
Da e ok. Am exagerat un pic ce-i drept dar „no harm done”. Eu ies. O sa ma gandesc daca am timp si chef mai pe seara la aplicatiile tale de la prb asta. Oricum sunt frumoase prb tale cel putin la prima vdr😀 Oricum bag de seama ca si dvs sunteti un ganditor bun (parca ar fi dialog intre platon si aristotel…u esti un ganditor bun….dar si u esti un bun ganditor) Si ca sa justific asta am vazut demonstratii interesante de-ale dvs pe site … nu multe ca ati intrat de curand pe site sau poate sunteti mai vechi oricum v-am vazut de putin timp.
Poti urmari si subiectul http://mathdiscovery.com/forum/viewtopic.php?f=5&t=49.Inca lucrez la el,cu cat vor mai aparea idei si materiale de referinta voi mai posta pe site.
2. Avem de pus 7 pct care sa aiba minim distanta 1/2 intre fiecare doua.
Punem primul pct f aproape de centru (deoarece daca l-am pune in centru ne-ar cam jena fiindca avem de mutat un punct din cele 2 aflate pe diametru..dar tot aici se ajunge). Celelalte 6 pct le punem in jurul cercului determinat de centrul patratului. Raza e 1/2. Astfel am construit cele 7 pct. se observa ca orice dreapta care trece prin centrul patratului imparte patratul in 2 parti o parte avand 3 pct cealalta 4. datorita acestui rationament nu putem avea 2 pct intr-o parte 5 in cealalta sau alte cazuri degenerate. Chiar daca dreapta care trece prin centru intalneste 2 pct distributia va fi 2 cu 3 si tot se gasesc 4 diagonale din „poligon” prin care trece aceasta dreapta. Cu cat indepartam primul pct de centrul cercului cu atat e mai rau deoarece e posibil sa nu mai gasim toate cele 7 pct de care avem nevoie (s-ar putea sa iasa unele dintre ele din patrat). Eu cred ca avem sanse chiar cu o dreapta de lungime 1 care ramane in patrat sa obtinem 4 segmente care se intersecteaza (si nu e nevoie sa treaca prin centru).