In triunghiul ABC, [BN] mediana, N apartine (AC). Dreapta determinata de mijlocul segmentului [BN] si A intersecteaza pe [BC] in E. Demonstrati ca BC=3BE.
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
In triunghiul ABC, [BN] mediana, N apartine (AC). Dreapta determinata de mijlocul segmentului [BN] si A intersecteaza pe [BC] in E. Demonstrati ca BC=3BE.
Notezi
intersectia lui 
cu 
. In triunghiul 
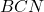cu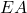 
secanta folosesti http://ro.wikipedia.org/wiki/Teorema_lui_Menelaus si obtii:
(q.e.d.)
Solutie fara teorema lui Menelaus.
Duc paralela NP la BC si paralela PM la AC. Acum PBMN devine paralelogram. Mai notez intersectia lui AE si NP cu G si intersectia lui BN si PM cu O. În triunghiul ABN, AO si NP sunt doua mediane, deci G este centrul sau de greutate, adica NG=2PG. Cum GN=BE, iar PG=EM, rezulta BE=2EM etc.