Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Se da triunghiul isoscel ABC,AB=AC=16radical din 5 cm,BC=32 cm si punctul M ce nu apartine planului (ABC) astfel incat MA=MB=MC=25 cm.Sa se afle:
a)raza cercului circumscris triunghiului ABC
b)distanta de la punctul M la planul (ABC)
c)distanta de la punctul M la dreapta BC
d)distanta de la punctul O (piciorul perpendicularei dusa din M pe planul (ABC) la planul (MBC)
e)tangenta unghiului format de planul (MBC) si (ABC)
a) Fie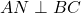
. Cum triunghiul este isoscel, N este mijlocul laturii BC. Aplicand teorema lui Pitagora in triunghiul ANC se obtine inaltimea AN=32.
Fie O centrul cercului circumscris, care se va afla pe AN. In triunghiul dreptunghic ONC, cu NC=16, OC=R, ON=32-R, unde R este raza cercului, se aplica Pitagora si se afla R.
b) In triunghiul MOA se aplica Pitagora si se afla MO.
c) Distanta de la M la BC este MN (se demonstreaza cu teorema celor 3 perpendiculare) si in triunghiul MON se aplica Pitagora
d) Distanta de la O la planul MBC este perpendiculara din O pe MN (trebuie sa demonstrezi) care este in acelasi timp inaltime in triunghiul MON
e) Unghiul diedru este MNO si se aplica tangenta in triunghiul dreptunghic MON.