aratati ca pt orice n natural avem:
![]()
este divizibil cu 4.
multumesc
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
ESTI SIGURA CA PROBLEMA ASTA NU TREBUIE POSTAT IN RUBRICA”CLASA A 9″???
Se rez folosind metoda inductiei.
se demonstreaza prin disjunctia cazurilor:
1.
2.
1.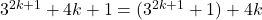

2.
Am dat si eu valori pana la n=4, si relatia este adev si pt nr pare si pt impare, dar nu am stiut sa generalizez.
Este sigur de clasa a 7, pt ca ne-a dat-o ca tema….
dan ai presupus ca e adev pt n=k si ai dem pt n=k+1, dar nu inteleg: daca pe baza unui lucru presupus demonstrezi alt lucru ca e adevarat, asta inseamna ca si lucrul presupus initial este adevarat?
in rest am priceput, e cam greu, dar a mers
multumesc