Calculați primitivele următoarelor funcții:
,
––
eu am încercat ceva la fiecare dar nu am ajuns la rezultatul final
pentru a) am notat x+1=u doar că am ajuns din nou la o integrală de prima formă – nu stiu daca a ajutat
b) am făcut o derivare prin părți și am ajuns la integrala
de aici n-am știut cum ar trebui făcută integrala
c)am amplificat și am ajuns la


1.Dupa substitutia ta obtinem:
^2\sqrt{u^2+1}du=\int(u^2-2u+1)\sqrt{u^2+1}du=\int(u^2+1)\sqrt{u^2+1}du-\int2u\sqrt{u^2+1}du)
+c) . De aceea vom face substitutia
. De aceea vom face substitutia ) .
.
Ne ocupam de prima integrala din diferenta. Este cunoscut faptul ca
Trebuie sa il aflam acum pe u in functie de noul y introdus. Stim ca) de unde rezulta ca
de unde rezulta ca ) .
.
Exponentiem cele 2 relatii pentru a obtine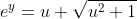 si
si }=\frac1{e^{\ln(u+\sqrt{u^2+1})}}=\frac1{u+\sqrt{u^2+1}}=\frac{u-\sqrt{u^2+1}}{u^2-u^2-1}=\sqrt{u^2+1}-u) .
.
Sczand realtiile obtinute, ramanem cu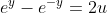 deci
deci 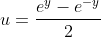 . Functia u se numeste sinus hiperbolic iar functia y de mai sus este inversa sinusului hiperbolic. Poti gasi mai multe informatii despre aceste functii hiperbolice pe wikipedia.
. Functia u se numeste sinus hiperbolic iar functia y de mai sus este inversa sinusului hiperbolic. Poti gasi mai multe informatii despre aceste functii hiperbolice pe wikipedia.
Deci facem substitutia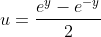 . Rezulta atunci ca
. Rezulta atunci ca 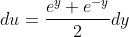 si deci integrala devine:
si deci integrala devine:
\sqrt{u^2+1}du=\int((\frac{e^y-e^{-y}}{2})^2+1)\sqrt{(\frac{e^y-e^{-y}}{2})^2+1}\cdot\frac{e^y+e^{-y}}{2}dy=\int((\frac{e^y-e^{-y}}{2})^2+1)\sqrt{(\frac{e^y-e^{-y}}{2})^2+1}\cdot\frac{e^y+e^{-y}}{2}\cdot&space;e^y\cdot&space;e^{-y}dy)
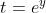 deci
deci 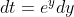 . Integrala devine:
. Integrala devine:
^2+1)\sqrt{((\frac{t-\frac1{t}}{2})^2+1)}\frac{t+\frac1{t}}2\cdot\frac1{t}dt)
^2+1=\frac{t^2+\frac1{t^2}-2}{4}+\frac44=\frac{t^2+\frac1{t^2}+2}{4}=(\frac{t+\frac1{t}}{2})^2) . Observam ca radicalul dispare!! Integrala devine:
. Observam ca radicalul dispare!! Integrala devine:
^2}{t^5}}dt=\frac1{16}\int{\frac{t^8+4t^6+6t^4+4t^2+1}{t^5}}dt=\frac1{16}\int&space;t^3+4t+6\frac1{t}+4\frac{1}{t^3}+\frac1{t^5}dt=\frac1{16}(\frac{t^4}{4}+2t^2+6\ln(t)+4\frac{t^{-2}}{-2}+\frac{t^{-4}}{-4})+c=\frac1{16}(\frac{t^4}{4}+2t^2-\frac2{t^2}-\frac{1}{4t^4}+6\ln(t))+c=\frac1{16}({\frac{t^8+8t^6-8t^2-1}{4t^4}}+6\ln(t))+c)
Mai departe facem substitutia evidenta(evidenta deoarece avem doar functii exponentiale; cei 2 termeni adaugati la final sunt pentru a face mai usoara substitutia)
Luam primul termen al integralei, care apare si sub radical si il prelucram:
Acum mai ramane sa facem substitutiile inapoi. Incepem cu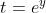 si obtinem:
si obtinem:
+c) . Urmeaza
. Urmeaza ) . Integrala devine:
. Integrala devine:
^8+8(u+\sqrt{u^2+1})^6-8(u+\sqrt{u^2+1})^2-1}{4(u+\sqrt{u^2+1})^4})+6\ln(u+\sqrt{u^2+1}))+c)
Mai ramane doar sa inlocuim u cu x+1 pentru a obtine integrala functiei date. Si sa speram ca nu am gresit niciun calcul 🙂
O alta idee de rezolvare este sa facem substitutia) .
.
Edit:Am uitat de a 2-a integrala din diferenta, dar aceea este usor de rezolvat(incepand prin substitutia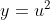 ).
).
2.Integrarea prin parti este o idee buna. Mai ramane sa rezolvam integrala . Amplificam cu x obtinand
. Amplificam cu x obtinand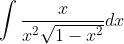 . Facem substitutia
. Facem substitutia 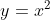 . Integrala este usor de rezolvat mai departe, daca mai ai nevoie de ajutor lasa un mesaj.
. Integrala este usor de rezolvat mai departe, daca mai ai nevoie de ajutor lasa un mesaj.
Făcând această substitutie nu vom ajuge la integrala de la care am pornit?
Te referi la a 2-a problema? Nu avem cum sa ajungem la integrala de la care am pornit deoarece am scos un termen din ea cand am integrat prin parti. Ajungem insa la urmatoarea integrala:
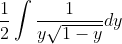 ce se poate rezolva spre exemplu prin substitutia
ce se poate rezolva spre exemplu prin substitutia 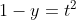 .
.
3.Facem substitutia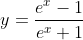 . Puteam lua chiar si tot radicalul in aceasta substitutie dar este mai simplu de facut asa. Scoatem pe x in functie de y:
. Puteam lua chiar si tot radicalul in aceasta substitutie dar este mai simplu de facut asa. Scoatem pe x in functie de y:
=e^x-1)
=-1-y)
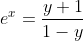
=\ln(y+1)-\ln(1-y))
dy=\frac{1-y+y+1}{(y+1)(1-y)}dy=\frac{2}{1-y^2}dy)
Derivand:
Integrala devine:
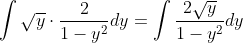
Mai departe facem substitutia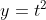 adica
adica 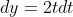 de unde avem:
de unde avem:
(1+t^2)}dt=4(\int\frac{t^2+1}{(1-t^2)(1+t^2)}dt-\int\frac1{(1-t^2)(1+t^2)}dt)=4(\int\frac1{1-t^2}dt-\frac12\int\frac{(1-t^2)+(1+t^2)}{(1-t^2)(1+t^2)}dt)=4(\int\frac1{1-t^2}dt-\frac12(\int\frac1{1+t^2}dt+\int\frac1{1-t^2}dt))=4\int\frac1{1-t^2}dt-2\int\frac1{1+t^2}dt-2\int\frac1{1-t^2}dt=2\int\frac1{1-t^2}dt-2\int\frac1{1+t^2}dt=2(\frac12\ln(\frac{t+1}{1-t}))-2\arctan(t)+c=\ln(\frac{t+1}{1-t})-2\arctan(t)+c)
Refacem substitutiile: , obtinand:
, obtinand:
-2\arctan(\sqrt\frac{e^x-1}{e^x+1})+c=\ln(\frac{\sqrt{e^x-1}+\sqrt{e^x+1}}{\sqrt{e^x-1}-\sqrt{e^x+1}})-2\arctan(\sqrt\frac{e^x-1}{e^x+1})+c)
Modul in care am refacut substitutiile e o confirmare a faptului ca puteam substitui direct tot radicalul.
Mulțumesc mult pentru ajutor!
La ex. 2 am scris eu greșit cand am facut substitutia. Am înțeles!
Cred ca la ex. 1 nu mi-ar fi venit niciodată acea idee!😄
Cu placere! Nici mie nu mi-ar fi venit ideea daca n-as mai fi vazut integrale asemanatoare.