Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
sa se demonstreze prin metoda inductiei matematice egalitatilor ex nr2: 1x2x3+2x3x4…+n(n+1)(n+2)=n(n+1)(n+2)(n+3) supra 4, n E N* ex nr 4: 1la put4+2la put4+3 la put4 +…=n la puterea 4=n(n+1)(2n+1)(3nla puterea4+3n-1) supra 30, n E N* ex 8:1supra1x3 +1supra3x5+….+1supra(2n-1)(2n+1)=n supra 2n+1, n E N* ex 9: 1 supra 1×4 + 1 supra 4×7 +…+ 1supra(3n-2)(3n+1)=nsupra 3n+1,n E N*
Posteaza si enunturile acestor exercitii.
daca nu se vede iti dau cerinta
am pus poza nu se vede?
Acum se vad.
1.Avem de demonstrat ca(n+2)=\frac{n(n+1)(n+2)(n+3)}{4})
.
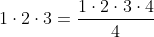
Pasul 1(verificare pentru n=1):
Se vede usor ca aceasta egalitate este adevarata
Pasul 2(demonstratia propriu-zisa). Presupunem ca propozitia este adevarata pentru k si demonstram ca atunci este adevarata si pentru k+1. Din faptul ca propozitia este adevarata pentru k stim ca:
(k+2)=\frac{k(k+1)(k+2)(k+3)}{4})
(k+2)(k+3))
obtinem:
(k+2)+(k+1)(k+2)(k+3)=\frac{k(k+1)(k+2)(k+3)}{4}+(k+1)(k+2)(k+3)=\frac{k(k+1)(k+2)(k+3)+4(k+1)(k+2)(k+3)}{4}=\frac{(k+1)(k+2)(k+3)(k+4)}{4})
Adunand
Aceasta este fix propozitia pentru k+1.
Rezulta din Principiul inducitiei matematice ca propozitia data este adevarata pentru orice n natural nenul.