Home/ Intrebari/Q 5673
Urmator
Answered

AniDeȘcoală.ro Latest Intrebari

mary-
5
Pe: 2021-03-10T13:59:36+02:00 In: In:

Să se determine cel mai mic termen …

Să se determine cel mai mic termen al sirului cu termenul general a_n=\frac{n^2}{3}-3n.
–

Pentru rezolvare m-am gândit inițial sa calculez a_{n+1}-a_n=\frac{2n-8}{3}
Insa nu se poate spune nimic despre monotonia sirului.

Ma gandeam eventual sa observ ca a_1>a_2>a_3\cdots
Insa nu stiu cum as putea determina cel mai mic termen..

Ceva idei? Mulțumesc!

Similare

3 raspunsuri

  1. Alexandru10
    Raspuns editat.

    Consideri functia f(x)=x2/3-3x
    f(x)=0 x1=0  , x2=3
    Deci pt x∈[0,3]   f(x) este negativa.Tragem concluziaa  ca  si   an este negativa pt n∈[0,3]
    pt n=0 si n=3 an este o
    Valori strict negative   se ia pt n=  1  si  2.Calculezi a1 si a2 sile compari.Pt alte valori ale lui n an>0
    a1=12/3-3*1=1/3-3= -8/3
    a2=22/3-3=4/3-3=-5/3
    -8/3<-5/3=> -8/3 valoarea minima a sirului

     

  2. Menim
    Best Answer
    Raspuns editat.

    Rezolvarea de mai sus este gresita. 3 nu este o radacina a functiei f. De asemenea o functie nu este echivalenta in general cu un sir.

    a_{n+1}-a_n=\frac{(n+1)^2-n^2}{3}-3(n+1)+3n=\frac{2n+1}{3}-3=\frac{2n-8}{3}, asa cum ai obtinut si tu.

    Observam ca daca n>4, atunci 2n-8>0, deci a_{n+1}-a_n>0. Rezulta ca pt n>4, a_{n+1}>a_n adica sirul creste.

    Daca n<4 atunci analog obtinem ca sirul descreste. Din aceste 2 observatii rezulta ca minimul sirului se obtine pentru n=4(sirul descreste pana la 4 si apoi de la 4 creste; poti sa iti imaginezi aceasta descrestere si crestere ca o coborare intr-o vale si urcare inapoi).

    Mai ramane as calculam termenul n=4:
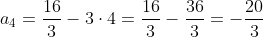
    a_4=\frac{16}3-3\cdot4=\frac{16}3-\frac{36}{3}=-\frac{20}{3}

Raspunde

Raspunde