Sa se arate ca restul impartirii a unui numar prim la 30 este de asemenea un număr prim sau egal cu 1. VA ROG SA EXPLICATI!
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
Sa se arate ca restul impartirii a unui numar prim la 30 este de asemenea un număr prim sau egal cu 1. VA ROG SA EXPLICATI!
Fie
un numar prim. Teorema impartirii cu rest ne spune ca exista 
si 
naturale astfel incat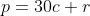 
, cu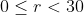 
.
In cazul in care numarul
este mai mic decat 30, atunci restul la impartirea cu 30 va fi desigur chiar 
, deci va fi prim.
In continuare ne ocupam de numerele prime mai mari decat 30. Ne reamintim ca numarul
este de forma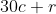 
. Daca 
este numar par, atunci 2 va fi un divizor al lui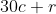 
si deci si al lui p. Dar atunci numarul nu va mai fi prim, deci 
nu poate fi par. Eliminand numerele pare(si reamintindu-ne ca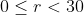 
), 
mai poate lua una din urmatoarele valori:
Daca
este multiplu de 3, atunci si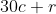 
va fi multiplu de 3, deci nu va mai fi prim. Eliminam deci si multiplii de 3 din lista de posibilitati, ramanand cu:
Restul nu poate fi 25, deoarece atunci numarul s-ar divide cu 5, deci nu ar mai fi prim. Singurele posibilitati care au ramas sunt 1, 5, 7, 11, 13, 17, 19, 23 si 29. Acestea sunt toate prime, in afara de 1, adica exact ceea ce s-a cerut.