Am nevoie de exercițiile 2,3,4,5. 
AniDeȘcoală.ro
Inregistrati-va pentru a beneficia de cunostintele comunitatii, a pune intrebari sau a a raspunde la intrebarilor celorlalti.
Suntem o comunitate care incurajeaza educatia si in care se intalnesc know-how-ul si experienta cu perspective inovative de abordare a problemelor.
Autentificati-va pentru a pune intrebari, a raspunde la intrebarilor celorlalti sau pentru a va conecta cu prietenii.
V-ati uitat parola ? Introduceti adresa de email si veti primi o noua parola.
Please briefly explain why you feel this question should be reported.
Va rugam explicate, pe scurt, de ce credeti ca aceasta intrebare trebuie raportata.
Motivul pentru care raportezi utilizatorul.
1.a)Vectorul pozitie are 2 componente, anume=4t-2)
si =-3t+1)
. Pentru a calcula ecuatia traiectoriei, formam sistemul \\y=y(t)&space;\end{matrix}\right.)
⇒ 
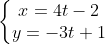, din care eliminam timpul, astfel:
b)Vectorul viteza se obtine derivand vectorul pozitiei in functie de timp:
c)^2}=\sqrt{16+9}=\sqrt{25}=5)
d)Acceleratia se obtine derivand vectorul viteza in functie de timp, sau altfel spus derivand vectorul pozitie de 2 ori in functie de timp. Daca ne uitam la vectorul viteza, observam ca niciuna din componentele lui nu depinde de timp, deci derivatele lor vor fi 0. Rezulta ca:
Modulul acceleratiei este si el 0.
2.a)Pentru a obtine ecuatia traiectoriei, eliminam timpul din ecuatiile miscarii.
⇒
⇒
⇒
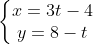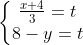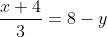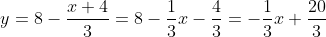
=\frac{dx}{dt}\vec&space;i+\frac{dy}{dt}\vec&space;j=\frac{d(3t-4)}{dt}\vec&space;i+\frac{d(8-t)}{dt}\vec&space;j=3\vec&space;i-\vec&space;j)
^2}=\sqrt{10})
=\vec{r_0}+\int_0^t&space;v(t)dt=4\vec&space;i-2\vec&space;j+\int_0^t(3\vec&space;i-4\vec&space;j)dt=4\vec&space;i-2\vec&space;j+3t\vec&space;i-4t\vec&space;j=(4+3t)\vec&space;i+(-2-4t)\vec&space;j)
b)Cele 2 componente ale vectorului miscare se obtin ca derivate in functie de timp ale celor 2 ecuatii ale miscarii:
c)
d)